The Relationship between Image Sensor Size and Aperture Value 絞り値と撮像センサーサイズとの関係

　絞り値（Aperture）はレンズの明るさを表す指標であり、使っている撮像センサーのサイズ（例えば1インチ、マクロフォーサーズ、APS-Cやフルサイズなど）とは関係ないものです。

　言い換えると、同じF2.8のレンズはフルサイズのカメラにつけても、コンバーターを付けて、APS-Cのカメラか、マイクロフォーサーズなどのカメラにつけても、F値としては全く変わりません。

　ただし、同じ焦点距離のレンズであれば、よく言われる「35㎜フィルム換算」の指標でいうときに、その換算した焦点距離は、撮像センサーのサイズと密接に関係します。

　レンズの焦点距離についての説明には、「深さ」（被写界深度）がつきものです。焦点距離が長ければ、深さは浅くなり、逆に短ければ、深さは深くなります。

　それは、写真の「ボケ」につながります。

　因みに、被写界深度の計算式は以下の通りだそうです[1]。

被写界深度＝前方被写界深度＋後方被写界深度前方被写界深度＝δ(F(s-f)^2/(f^2+δF(s-f))
後方被写界深度＝δF(s-f)^2/(f^2-δF(s-f))

ここでは、
　　F：　　F値 (撮影時の絞り)
　　ｓ：　　被写体距離[mm]
　　ｆ： 　レンズ焦点距離[mm]
　　δ： 　許容錯乱円直径 [mm]

　つまり、被写界深度は焦点距離、被写体までの距離、F値と許容錯乱円直径にしか関係ないです。

　以下の図はFが2.0のときに、被写界深さと被写体距離との関係を示します。

　後方被写界深度より、前方の方は浅いことは分かります。だから、パンフォーカス写真を撮るコツは、「約前方三分の一」の方に合わせるというコツがあるわけです。

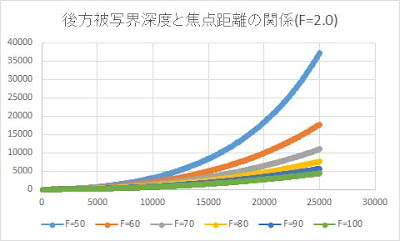
　以下の図は、Fが2.0であるときの、後方被写界深度と焦点距離との関係を示します。25メートル先の被写体については、焦点距離が100mmの深さが約4.3mに対して、50㎜のは約37mです。つまり、約8.5倍です。同様の比較としては、5m先ですと、約4.5倍になります。

さらに、焦点距離の比較範囲を600㎜まで増やし、被写体までの距離を5mまで限定して、後方被写界深度と焦点距離と比較してみると、以下の図になります。

つまり、５ｍ先のものですと、300㎜の深さは約14㎜に対して、600㎜は約3㎜しかありません！

　ところで、ボケ具合は「実有効口径」と関係すると言われます。ややこしいが、深さは以上の計算では問題ありませんが、有効口径となると、以下の式で計算されるが、撮像センサーのサイズによる「換算」ではなく、レンズの焦点距離そのものを使います。
　　有効口径＝レンズの焦点距離÷開放ｆ値

　となると、換算した焦点距離（実際は画角となるが）が変わっていても、ボケの具合は変わらないことになります。

　もちろん、同じ焦点距離であれば、解放F値が小さければ小さいほど、ボケが大きいことにはなります。

---

参考リンク：
[1] 被写界深度に関する計算式